Terminal Velocity
Problems from IIT JEE
Problem (IIT JEE 2015):
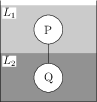 Two spheres P and Q of equal radii have densities $\rho_1$ and $\rho_2$, respectively. The spheres are connected by a massless string and placed in liquids $L_1$ and $L_2$ of densities $\sigma_1$ and $\sigma_2$ and viscosities $\eta_1$ and $\eta_2$, respectively. They float in equilibrium with the sphere P in $L_1$ and sphere $Q$ in $L_2$ and the string being taut (see figure). If sphere P alone in $L_2$ has terminal velocity $\vec{v}_\text{P}$ and Q alone in $L_1$ has terminal velocity $\vec{v}_\text{Q}$, then,
Two spheres P and Q of equal radii have densities $\rho_1$ and $\rho_2$, respectively. The spheres are connected by a massless string and placed in liquids $L_1$ and $L_2$ of densities $\sigma_1$ and $\sigma_2$ and viscosities $\eta_1$ and $\eta_2$, respectively. They float in equilibrium with the sphere P in $L_1$ and sphere $Q$ in $L_2$ and the string being taut (see figure). If sphere P alone in $L_2$ has terminal velocity $\vec{v}_\text{P}$ and Q alone in $L_1$ has terminal velocity $\vec{v}_\text{Q}$, then,
- $\frac{|\vec{v}_\text{P}|}{|\vec{v}_\text{Q}|}=\frac{\eta_1}{\eta_2}$
- $\frac{|\vec{v}_\text{P}|}{|\vec{v}_\text{Q}|}=\frac{\eta_2}{\eta_1}$
- $\vec{v}_\text{P}\cdot\vec{v}_\text{Q}>0$
- $\vec{v}_\text{P}\cdot\vec{v}_\text{Q}<0$
Solution:
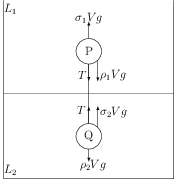 Let $V=\frac{4}{3}\pi r^3$ be the volume of the spheres P and Q of equal radii $r$. The forces acting on the sphere P are its weight $\rho_1Vg$, tension from the string $T$, and the buoyancy force $\sigma_1 Vg$ (see figure). Similarly, forces on the sphere Q are $\rho_2Vg$, $T$, and $\sigma_1 Vg$. In equilibrium, the net force on the spheres P and Q are separately zero i.e.,
\begin{align}
\label{ezb:eqn:1}
&T+\rho_1 V g=\sigma_1 Vg,\\
\label{ezb:eqn:2}
&T+\sigma_2 V g=\rho_2 Vg.
\end{align}
The tension $T>0$ because the string is taut. Thus, first equation gives $\rho_1<\sigma_1$ and second equation gives $\rho_2>\sigma_2$. Eliminate $T$ from first and second equation to get,
\begin{align}
\label{ezb:eqn:3}
\sigma_1-\rho_1=\rho_2-\sigma_2.
\end{align}
Let $V=\frac{4}{3}\pi r^3$ be the volume of the spheres P and Q of equal radii $r$. The forces acting on the sphere P are its weight $\rho_1Vg$, tension from the string $T$, and the buoyancy force $\sigma_1 Vg$ (see figure). Similarly, forces on the sphere Q are $\rho_2Vg$, $T$, and $\sigma_1 Vg$. In equilibrium, the net force on the spheres P and Q are separately zero i.e.,
\begin{align}
\label{ezb:eqn:1}
&T+\rho_1 V g=\sigma_1 Vg,\\
\label{ezb:eqn:2}
&T+\sigma_2 V g=\rho_2 Vg.
\end{align}
The tension $T>0$ because the string is taut. Thus, first equation gives $\rho_1<\sigma_1$ and second equation gives $\rho_2>\sigma_2$. Eliminate $T$ from first and second equation to get,
\begin{align}
\label{ezb:eqn:3}
\sigma_1-\rho_1=\rho_2-\sigma_2.
\end{align}
 Now, consider the situation when the sphere P moves in liquid $L_2$ and the sphere Q moves in liquid $L_1$. These spheres will attain the terminal velocities $\vec{v}_\text{P}$ and $\vec{v}_\text{Q}$ after some time. The direction of the velocity (upwards or downwards) will depend on the density of the sphere in comparison to the density of the liquid. Let us consider the case when $\rho_1>\sigma_2$. In this case, the velocity of the sphere P is downwards. From above equation, if $\rho_1>\sigma_2$ then $\rho_2<\sigma_1$. If the density of a sphere is less than the density of the liquid in which it is immersed, it will move up. Thus, the velocity of the sphere Q is upwards i.e., the directions of $\vec{v}_\text{P}$ and $\vec{v}_\text{Q}$ are opposite (see figure). Hence, $\vec{v}_\text{P}\cdot\vec{v}_\text{Q}<0$. The forces on the sphere P are its weight $\rho_1Vg$, buoyancy force $\sigma_2 Vg$, and viscous drag $6\pi \eta_2 r v_\text{P}$ (see figure). Similarly, the forces on the sphere Q are $\rho_2Vg$, $\sigma_1 Vg$ and $6\pi \eta_1 r v_\text{Q}$. Net forces on the spheres are zero when they move with terminal velocities i.e.,
\begin{align}
\label{ezb:eqn:4}
&6\pi\eta_2 r v_\text{P}+\rho_1 V g=\sigma_2 V g,\\
\label{ezb:eqn:5}
&6\pi\eta_1 r v_\text{Q}+\sigma_2 V g=\rho_1 V g.
\end{align}
Simplify above equations to get,
\begin{align}
\label{ezb:eqn:6}
&v_\text{P}=\frac{2 r^2 (\rho_1-\sigma_2)}{9\eta_2},\\
\label{ezb:eqn:7}
&v_\text{Q}=\frac{2 r^2 (\sigma_1-\rho_2)}{9\eta_1}.
\end{align}
Divide to get,
\begin{align}
\frac{|\vec{v}_\text{P}|}{|\vec{v}_\text{Q}|}=\frac{\eta_1}{\eta_2}\;\frac{\rho_1-\sigma_2}{\sigma_2-\rho_2}=\frac{\eta_1}{\eta_2}.
\end{align}
The readers are encouraged to show the results for the case $\rho_1<\sigma_2$.
Now, consider the situation when the sphere P moves in liquid $L_2$ and the sphere Q moves in liquid $L_1$. These spheres will attain the terminal velocities $\vec{v}_\text{P}$ and $\vec{v}_\text{Q}$ after some time. The direction of the velocity (upwards or downwards) will depend on the density of the sphere in comparison to the density of the liquid. Let us consider the case when $\rho_1>\sigma_2$. In this case, the velocity of the sphere P is downwards. From above equation, if $\rho_1>\sigma_2$ then $\rho_2<\sigma_1$. If the density of a sphere is less than the density of the liquid in which it is immersed, it will move up. Thus, the velocity of the sphere Q is upwards i.e., the directions of $\vec{v}_\text{P}$ and $\vec{v}_\text{Q}$ are opposite (see figure). Hence, $\vec{v}_\text{P}\cdot\vec{v}_\text{Q}<0$. The forces on the sphere P are its weight $\rho_1Vg$, buoyancy force $\sigma_2 Vg$, and viscous drag $6\pi \eta_2 r v_\text{P}$ (see figure). Similarly, the forces on the sphere Q are $\rho_2Vg$, $\sigma_1 Vg$ and $6\pi \eta_1 r v_\text{Q}$. Net forces on the spheres are zero when they move with terminal velocities i.e.,
\begin{align}
\label{ezb:eqn:4}
&6\pi\eta_2 r v_\text{P}+\rho_1 V g=\sigma_2 V g,\\
\label{ezb:eqn:5}
&6\pi\eta_1 r v_\text{Q}+\sigma_2 V g=\rho_1 V g.
\end{align}
Simplify above equations to get,
\begin{align}
\label{ezb:eqn:6}
&v_\text{P}=\frac{2 r^2 (\rho_1-\sigma_2)}{9\eta_2},\\
\label{ezb:eqn:7}
&v_\text{Q}=\frac{2 r^2 (\sigma_1-\rho_2)}{9\eta_1}.
\end{align}
Divide to get,
\begin{align}
\frac{|\vec{v}_\text{P}|}{|\vec{v}_\text{Q}|}=\frac{\eta_1}{\eta_2}\;\frac{\rho_1-\sigma_2}{\sigma_2-\rho_2}=\frac{\eta_1}{\eta_2}.
\end{align}
The readers are encouraged to show the results for the case $\rho_1<\sigma_2$.
